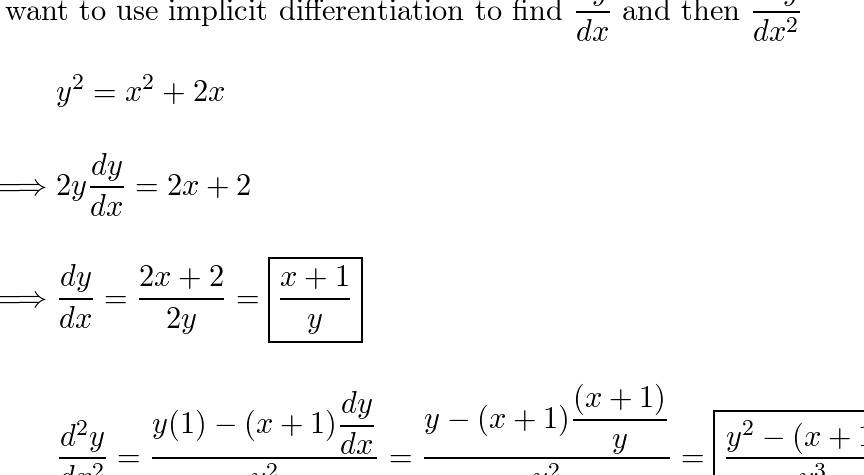Los derivados tienen muchos usos además de las matemáticas y la vida cotidiana, incluso en materias como ciencia, ingeniería, física y otras.
Debe haber dominado la capacidad de calcular la derivada de varias funciones en cursos anteriores, incluidas trigonométricas, implícitas, logarítmicas, etc.
d2y/dx2 y (dydx)^2 son dos ecuaciones derivadas. Pero para entenderlos, primero, necesitas entender qué es exactamente la segunda derivada.
La derivada de una función en cálculo se conoce como la segunda derivada, a veces conocida como la derivada de segundo orden.
La segunda derivada, en términos generales, mide cómo cambia la tasa de cambio de una cantidad. Por ejemplo, la segunda derivada de la posición de un objeto con respecto al tiempo es la aceleración instantánea del objeto o la velocidad a la que cambia la velocidad del objeto con respecto al tiempo.
En este artículo, te diré cuál es la diferencia entre d2y/dx2=(dydx)^2 y qué significa exactamente derivada.
D2y/dx2 contra (dydx)^2
Derivado de dy/dx (Estos 2 pueden parecer una notación de índice, pero no lo son). (dydx)2, por otro lado, es el cuadrado de la primera derivada.
Ejemplo:
Toma Y=3????3+6????2y=3×3+6×2
La primera derivada: dy/dx=9????2+12????dydx=9×2+12x
La segunda derivada: d2yd????2=18????+12d2ydx2=18x+12
El cuadrado de la primera derivada: (dydx)2=(9????2+12????)2=(81????4+216????3+144
¿Qué es la segunda derivada?
Cuando derivas la derivada, obtienes el segunda derivada. Recuerda que dy/dx es la derivada de y con respecto a x. La segunda derivada, pronunciada “dee dos y por dx al cuadrado”, se representa como d2y/dx2.
La naturaleza de los puntos estacionarios se puede determinar más fácilmente utilizando la segunda derivada (ya sean puntos máximos, puntos mínimos o puntos de inflexión).
Cuando dy/dx = 0, una curva llega a un punto estacionario. El tipo de punto estacionario (máximo, mínimo o punto de inflexión) se puede determinar mediante la segunda derivada una vez establecida la ubicación del punto estacionario.
d2y/d2x=PositivoEs un punto mínimo d2y/d2x=NegativoEs un punto máximo d2y/d2x Igual a ceroEs tanto un punto mínimo como un máximo d2y/d2x=0Prueba los valores de dy/dx a ambos lados del punto estacionario, como antes en el estacionario sección de puntos¿Cómo se identifican los puntos máximos y mínimos?
 d2y/d2x es la segunda derivada.
d2y/d2x es la segunda derivada.
¿Qué es derivado?
Él derivado de una función de una variable real en matemáticas cuantifica la sensibilidad del valor de la función (valor de salida) a los cambios en su argumento (valor de entrada). La herramienta principal del cálculo es la derivada.
La velocidad de un objeto, por ejemplo, es la derivada de su posición con respecto al tiempo. Cuantifica la rapidez con la que varía la posición del objeto a medida que pasa el tiempo.
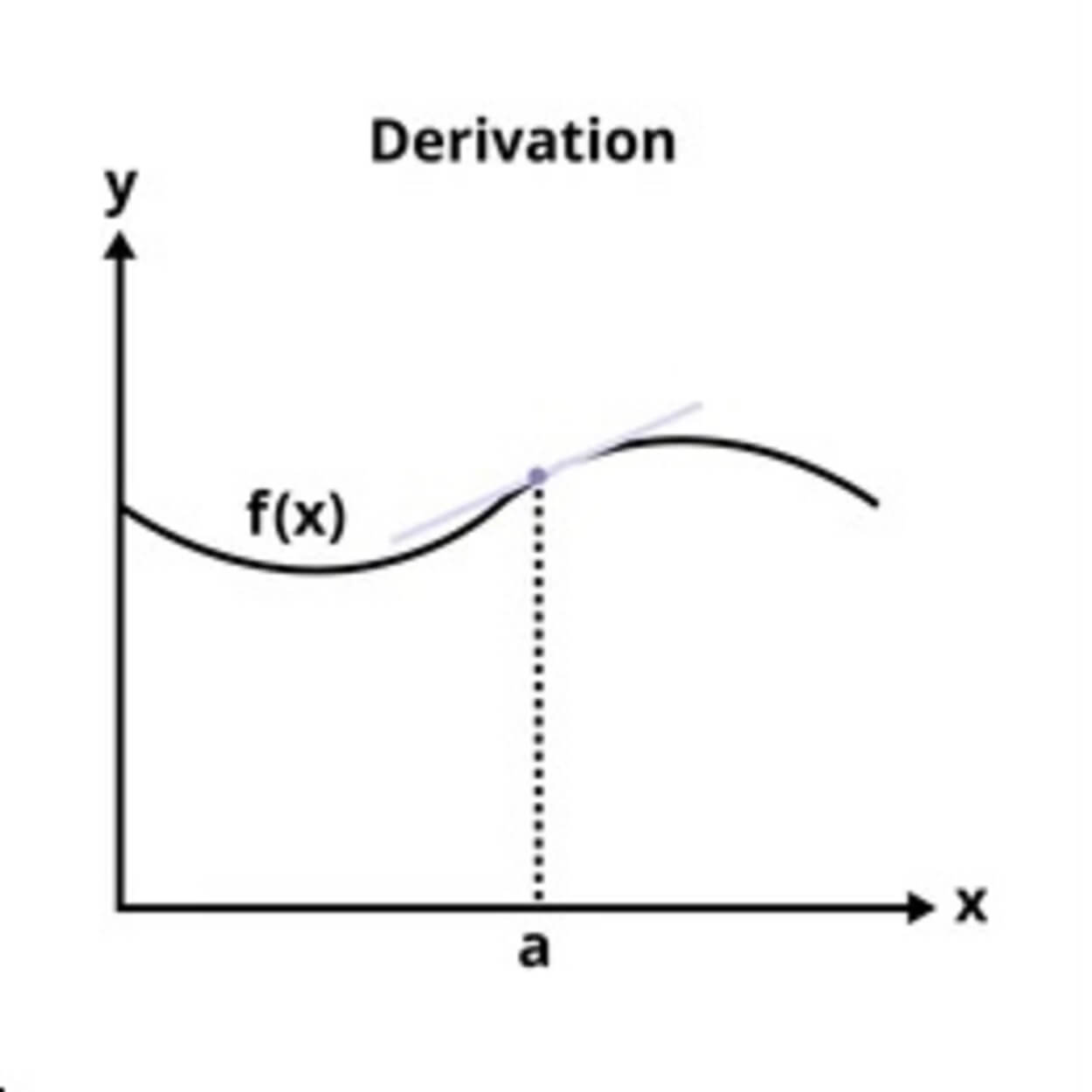
Cuando ocurre, la pendiente de la linea tangente al gráfico de la función en un valor de entrada dado es la derivada de una función de una sola variable. La función más cercana a ese valor de entrada se aproxima mejor linealmente mediante la línea tangente.
Debido a esto, la derivada se denomina con frecuencia «tasa de cambio instantánea«, que es la relación entre el cambio instantáneo en la variable dependiente y el de la variable independiente.
Para incluir funciones de varias variables reales, las derivadas pueden generalizarse. Esta generalización reinterpreta la derivada como una lineal transformación cuya gráfica, después de una traslación adecuada, es la mejor aproximación lineal a la gráfica de la función original.
En cuanto al fundamento proporcionado por la selección de variables independientes y dependientes, la matriz jacobiana es la matriz que representa esta transformación lineal.
Se puede calcular usando las derivadas parciales de las variables independientes. El vector gradiente reemplaza la matriz jacobiana por una función de valor real con varias variables.
La diferenciación es la acción de localizar una derivada. Antidiferenciación es el término para el proceso opuesto. La antidiferenciación y la integración están relacionadas en el teorema fundamental del cálculo. Las dos operaciones fundamentales del cálculo de una sola variable son la diferenciación y la integración.
Mire este video para conocer las derivadas y la función de una variable real
Notaciones diferentes
notación de leibniz
En 1675, Gottfried Wilhelm Leibniz introdujo las letras dx, dy y dy/dx. Incluso hoy en día, se emplea con frecuencia cuando la relación entre las variables dependientes e independientes en la ecuación y = f(x) se considera funcional.
La variable de diferenciación (en el denominador) se puede especificar usando la notación de Leibniz, que es importante para la diferenciación parcial.
notación de Lagrange
Una de las notaciones de diferenciación modernas más populares, a veces conocida como notación prima, usa la marca prima y se acredita a Joseph-Louis Lagrange. Denota la derivada de una función f como f1.
La última notación se generaliza para proporcionar la notación f(n) para la n-ésima derivada de f, lo cual es más conveniente cuando se analiza la derivada como una función en lugar de una función de sí misma porque la notación de Leibniz puede ser complicada en esta situación.
notación de newton
Se coloca un punto sobre el nombre de la función en Notación de diferenciación de Newtona menudo conocida como la «notación de puntos», para significar una derivada de tiempo.
Solo las derivadas con respecto al tiempo o la longitud del arco se representan utilizando esta notación. Por lo general, se aplica a ecuaciones diferenciales en geometría diferencial y física. Sin embargo, la notación de puntos no es aplicable a varias variables independientes y derivadas de alto orden (orden 4 o más).
notación de Euler
La primera derivada Df se obtiene usando el operador diferencial D en notación de Euler aplicándolo a una función f. Dnd representa la n-ésima derivada.
Si y = f(x) es una variable dependiente, la variable independiente x se aclara con frecuencia agregando el subíndice x a la D.
Aunque cuando se entiende la variable x, como cuando ésta es la única variable independiente contenida en la ecuación, frecuentemente se omite este subíndice.
Para expresar y resolver ecuaciones diferenciales lineales, la notación de Euler es útil.
Aplicación de Derivadas en Matemáticas
Los derivados se utilizan con frecuencia en matemáticas. Se pueden utilizar para determinar el máximo o mínimo de una función, la pendiente de una curva o incluso el punto de inflexión.
A continuación se muestran algunos casos en los que usaremos la derivada. Y las siguientes secciones entran en gran detalle sobre cada uno de ellos. La aplicación de derivados se encuentra con mayor frecuencia en:
- Cálculo de la tasa de cambio de una cantidad
- Obtener una buena estimación del valor
- Encontrar la ecuación para la tangente y la normal de una curva
- Identificar el punto de inflexión, máximos y mínimos
- Hacer una evaluación de las funciones crecientes y decrecientes
 Se utiliza una derivada para calcular el punto de inflexión, punto máximo y mínimo
Se utiliza una derivada para calcular el punto de inflexión, punto máximo y mínimo
Aplicación de Derivadas en la Vida Real
Los derivados se pueden utilizar en muchas situaciones en vida real. Aquí hay una lista de algunas situaciones en las que puede usar la derivación:
- Para calcular la ganancia y la pérdida en el negocio.
- Para medir la variación de temperatura.
- Para calcular la tasa de viaje, como millas por hora, kilómetros por hora, etc.
- Numerosas ecuaciones físicas se derivan usando derivadas.
- Encontrar el rango de magnitud de los terremotos es una tarea favorita en la investigación sismológica.
Conclusión
- d2y/dx2 es la segunda derivación.
- (dy/dx) ^2 es la primera derivada al cuadrado.
- Un derivado se usa en varios campos para varios propósitos en la vida real.
- Una derivada se usa en matemáticas para calcular puntos máximos y mínimos.
- Se puede utilizar en los negocios para calcular las finanzas del negocio y para calcular las pérdidas y ganancias.
Otros artículos